Continental Hotspot

Renzo’s rule is named after astronomer Renzo Sancisi (it is sometimes also called Sancisi’s law) who stated it thereby summarizing a large part of his carreer. It reads:

“When you see a feature in the light, you see a corresponding feature in the rotation curve.”

Now this makes obvious sense when we are dealing with Newtonian gravity because there the distribution of the matter, as measured by the emitted light, and the movement of that matter is directly linked through Newton’s law of gravity.

However when we are dealing with galaxies it is much less obvious that this rule should hold. Sure from the perspective of MOND it makes perfect sense because just like in Newtonian gravity there’s a direct link between the two quantities. From the perspective of dark matter on the other hand it doesn’t make much sense. To see why let’s look at the galaxy NGC 1560 which gives a great example of Renzo’s rule:

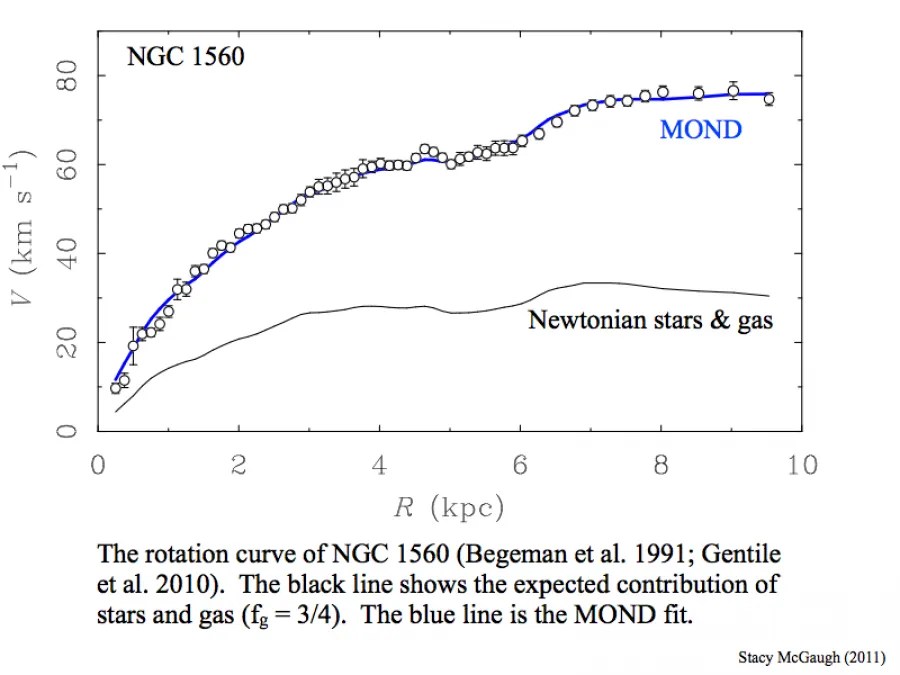
In this graph we see data points that represent measurements of the rotation speed of the galaxy. The thin black line represents the expected rotation speed of the galaxy based on the observed stars and gas from Newtonian gravity. The blue line shows the expected rotation curve from the mass distribution using Milgromian instead of Newtonian gravity.

In particular pay attention to the section of the graph at a radius of about 5 kiloparsecs. What is happening here is that there is a distinct dip in the Newtonian expected rotational velocity. This is caused by a local absence of matter, specifically gas. This region has been highlighted in the plots of the same galaxy below. In the left hand plot below we see that there is a local decrease in the gas density around 5kpc (green is gas, light blue is stars). This same dip is also seen in the rotation curve.

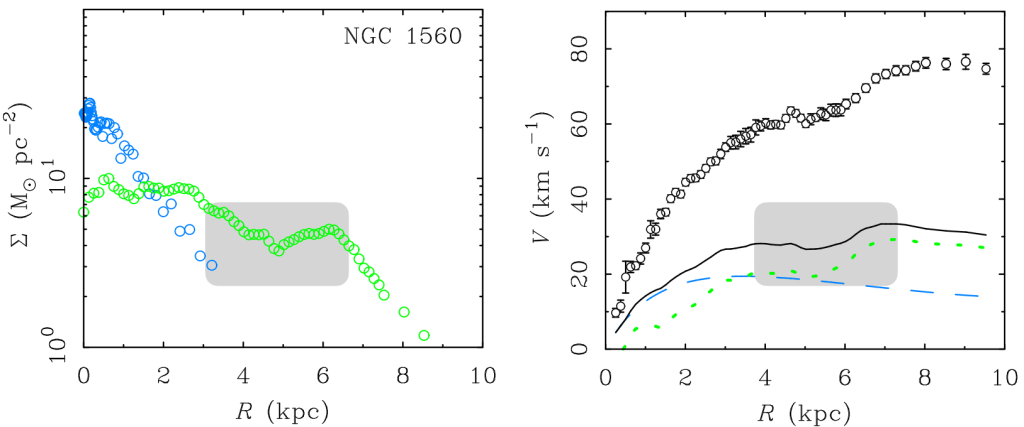
This is really weird from the dark matter perspective. If one accepts Newtonian gravity and infers that there is dark matter and one further supposes that the dark matter is smoothly distributed as almost all dark matter models do, then the rotation curve shouldn’t care about the details of the matter distribution such as this dip at 5kpc. In this view there is much more dark matter than ordinary matter so the contribution of ordinary matter to the rotation curve should be negligible. And yet the dip is clearly visible in the rotation curve. From the MOND perspective the dip makes perfect sense because the observed rotation curve is just the Newtonian expected rotation curve multiplied by the MOND interpolation function which just happens to be larger than 1 in this case.

In short the distribution of ordinary matter seems to dictate the movement of that ordinary matter, even when from a dark matter perspective it should be the smoothly distributed dark matter halo that governs the movements. In MOND however the match between the distribution of ordinary matter and the rotation curve is not just expected, it is required.