Continental Hotspot

MOND does not violate energy-momentum conservation and hasn’t ever since Milgrom and Bekenstein wrote down the AQUAL Lagrangian in 1984. This is one of two Lagrangians for MOND, the second being the QUMOND Lagrangian defined by Milgrom in 2010. So anyone who claims MOND violates energy-momentum conservation is now more than 40 years behind the times.

This article presents the field equations based on QUMOND and not AQUAL or some modified inertia version of MOND since QUMOND makes the Newtonian gravitational field explicit and hence is probably more easily understood. This version has also become the most popular for simulations and complicated analyses because QUMOND is much simpler to work with numerically. AQUAL and QUMOND have the same limits and produce the same behaviour in almost all cases, although they may differ up to 15% in unsymmetric cases, especially with characteristic accelerations around a₀.

Conservation laws

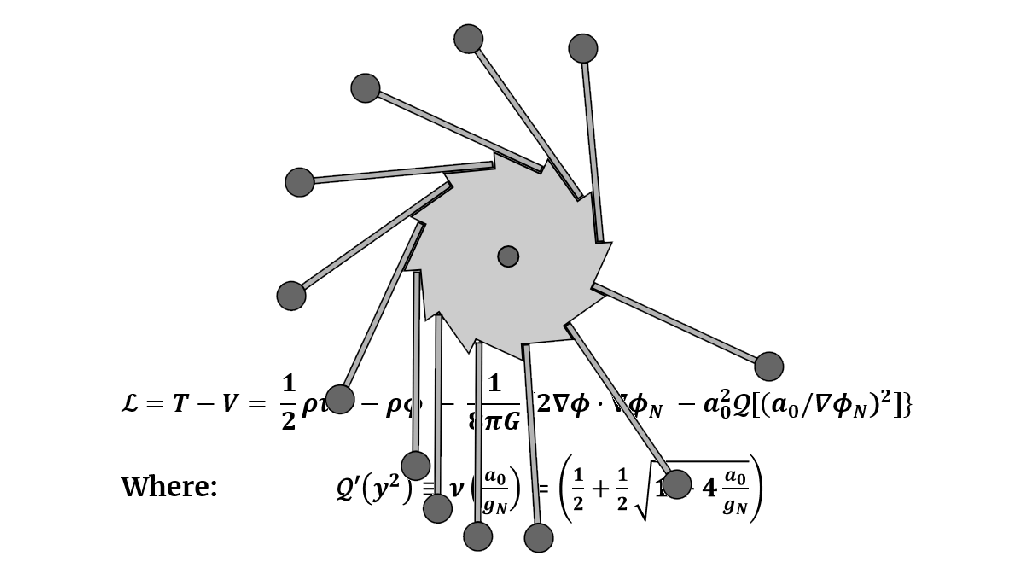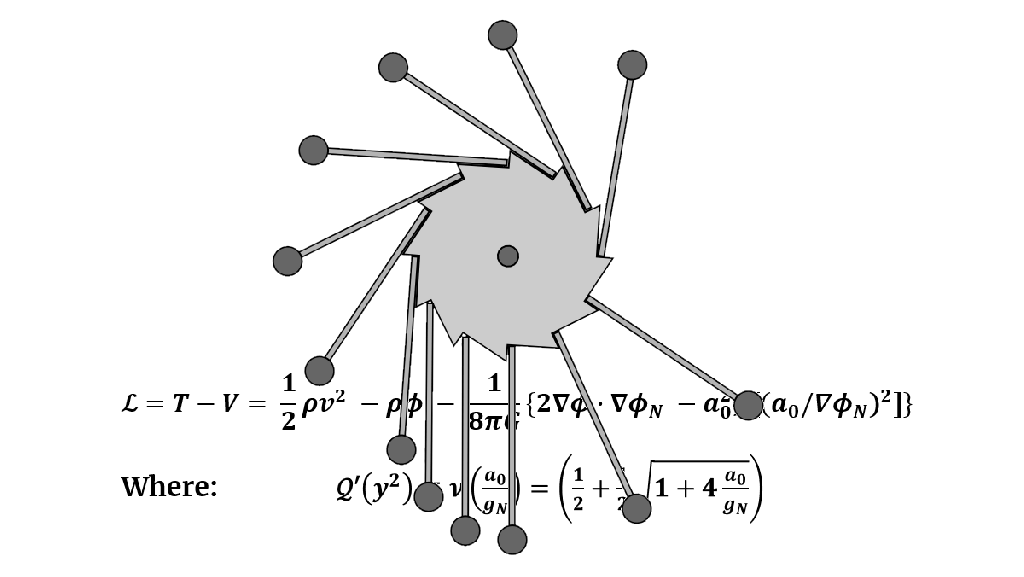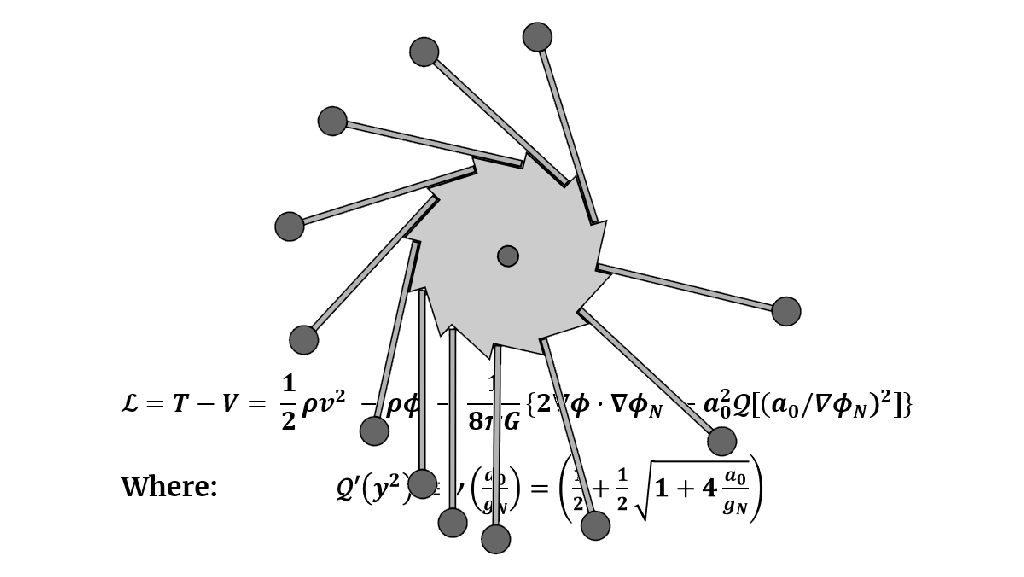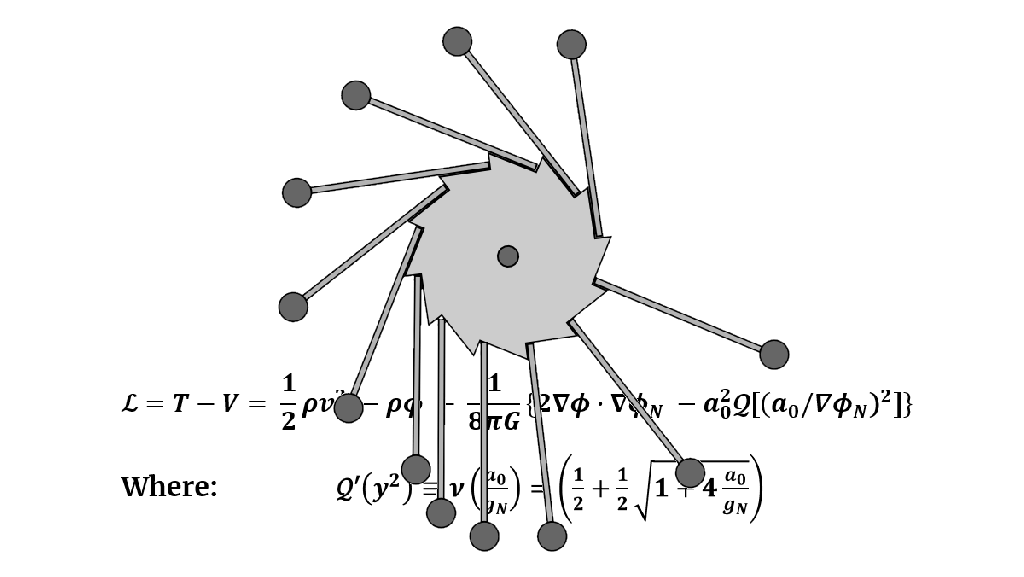
The QUMOND Lagrangian equals:

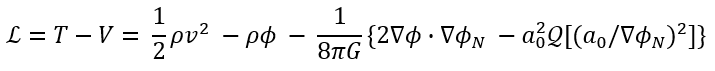
Energy conservation

As the Lagrangian does not explicitly depend on time (∂L/∂t=0), the energy is conserved following Noether’s theorem.

Momentum conservation

According to Noether’s theorem, momentum is conserved if the action is invariant under spatial translations xⁱ→xⁱ+ϵⁱ. This means that the Lagrangian density L must not explicitly depend on spatial coordinates xⁱ, but only on fields and their derivatives. As can be seen from the equation above the only variables are ρ, v, ∇ϕ and ∇ϕ_N with a₀ being a constant and Q being an algebraic function not dependent on ​xⁱ. Hence momentum is conserved.

Weak equivalence principle

This shows that MOND obeys the weak equivalence principle (WEP). And as long as one’s experiment is small/local also the Einstein equivalence principle (EEP). See also the article on the equivalence principle and MOND.

The Poisson equation

The derivation of the Poisson equation for the Newtonian auxiliary gravitational field is straightforward and identical to the derivation in ordinary Newtonian gravity:

This shows that in QUMOND one has the standard Poisson’s equation as an auxiliary field equation. It is used to calculate the MOND potential ϕ.

MOND field equation

The Lagrangian does not explicitly depend on ϕN therefore the first term in the Euler-Lagrange equation is zero. So let’s focus on the second term. The derivation proceeds as follows:

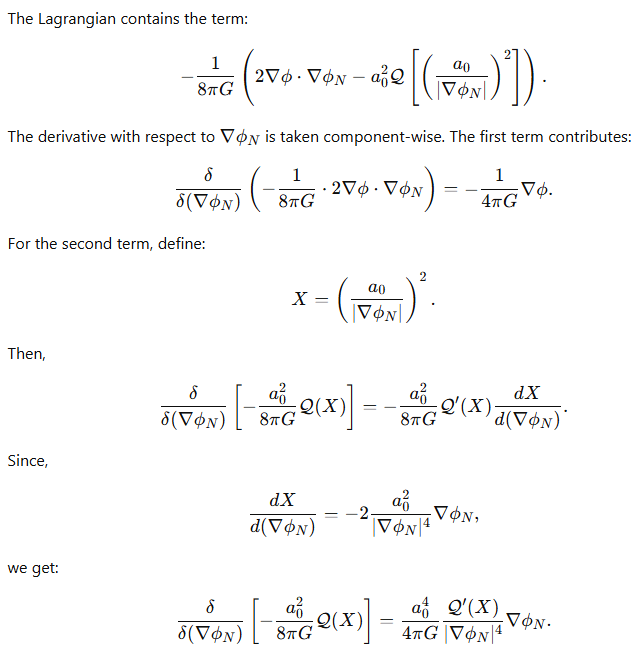
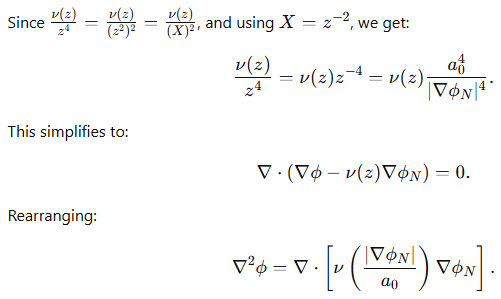
This finally is our QUMOND field equation relating the real Milgromian gravitational field to the Newtonian auxiliary gravitational field (which is just a calculational tool).

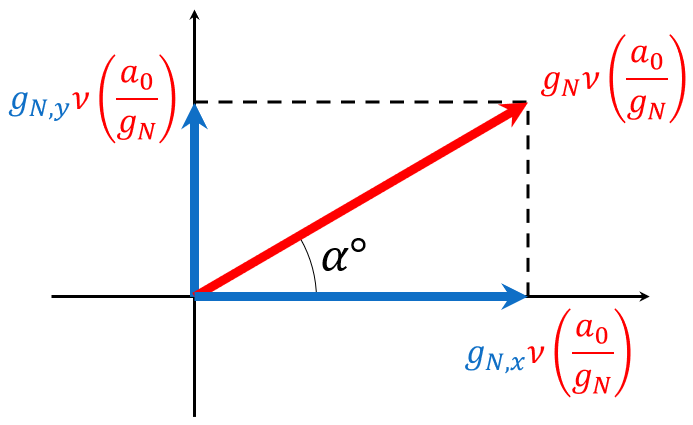
How to decompose vectors

An important side note in regards to these Lagrangian formulations is that the MOND interpolation function is applied along the direction the Newtonian gravitational field is pointing. Because the interpolation functions are nonlinear we cannot decompose the gravitational field along any arbitrary axes calculate interpolation functions for the components and then add everything back up. The values of the interpolation function for each component would not be the same as the value for the field in general. Therefore to calculate the Milgromian expectation one needs to calculate the interpolation function for gN along the direction it is pointing and then apply that same interpolation function to its components as is displayed here: