Short answer: no, they actually show what MOND expects.
The strength of gravity can be measured in the lab using a Cavendish experiment (see the diagram on the right). The idea is to suspend two test masses on a wire between two other large masses. Gravity will pull the balls together thereby twisting the wire. If you know how stiff the wire is and measure how far the balls move you can test the force of gravity.

So that is precisely what Gundlach et al. did. They found that even down to accelerations as low as 5×10-14 m/s2, which is more than a thousand times smaller than a0, there wasn’t any sign of a change in Newton’s laws.
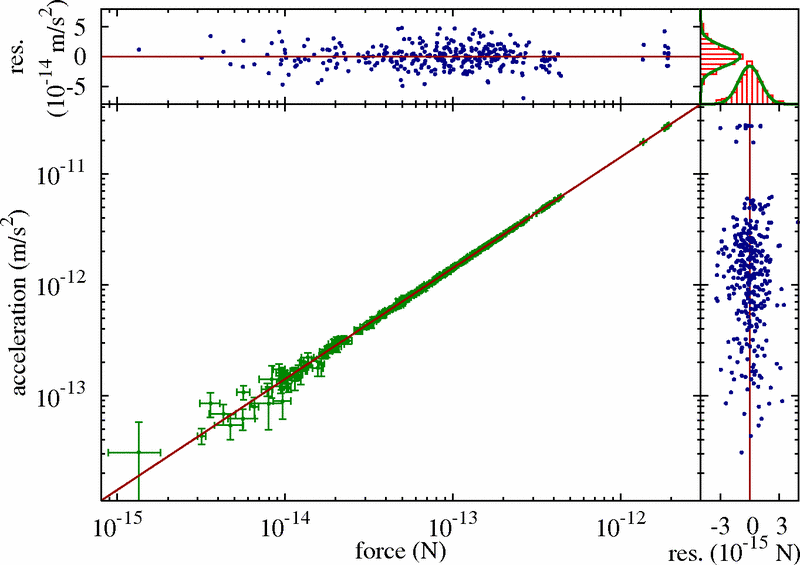
Gundlach et al. were very thorough in setting up their experiment. They used the University of Washington’s equivalence principle apparatus which you can see on the right. It is very carefully machined, is suspended on a very thin wire and operates in a vacuum. They also controlled for the heating of the apparatus due to friction in the torsion wire as the test was ongoing.

Independent confirmation
The results by Gundlach et al. are independent confirmation of earlier work by Little & Little who showed the same behaviour down to accelerations of 10-12 m/s2.

So that kills MOND right? Well, no. As you might have already guessed if you’ve read the post on the external field effect, these are exactly the results one expects in MOND. In MOND the gravity only becomes stronger than the Newtonian expectation once the total gravitational field drops below a0. And this experiment and others like it are happening on Earth. The gravitational field of the Earth at the surface is about 9.8 m/s2 which is eleven orders of magnitude larger. Even though the internal gravitational accelerations in the experiment are tiny the external field is very large. So according to MOND we shouldn’t see any modification of gravity. The external field puts us very far into the forced Newtonian limit of MOND.
Indeed in their conclusion Gundlach et al. mention this issue where they point out that their results do not disprove MOND as a modification of gravity (because of the external field effect):
“Our test does not invalidate MOND directly, since MOND requires that the measurement must be carried out in the absence of any other larger accelerations, such as those due to the Earth and our solar system. However, our results constrain any theoretical formalism seeking to derive MOND from fundamental principles by requiring that formalism to reproduce F=ma under laboratory conditions similar to those in our experiment.”
They do however conclude that they can rule out MOND as a theory of modified inertia. MOND as modified inertia hasn’t been discussed in this guide before but it basically means that the gravity stays the same but that objects respond to that gravity differently (and to other forces). This is not a popular approach to solving the astronomical discrepancies in galaxies, clusters, etc. because it poses even greater challenges than finding better equations for gravity or finding dark matter particles. Inertia is the resistance you feel when you try to push an object (even if friction to the ground is negligible). If you change the laws for that all sorts of experiments on Earth would also be expected to show discrepant results, everything from electricity and magnetism to radioactive decay and the structure of atoms would be affected. We don’t see anything funny happening in those types of experiments so it is safe to say that inertia isn’t modified.
In their paper Gundlach et al. also mention as an aside that while their experiment (and others like it) tests gravity, it also simultaneously tests the electromagnetic force. The wire on which the test masses are suspended twists and its stiffness counteracts gravity. This stiffness is due to electromagnetic forces in the wire. One might then imagine that gravity is somehow different but that this difference is being hidden exactly by a change in how wires behave. Gundlach et al. reasonably dismiss this as unlikely and overly complicated thinking though. Not only would that idea violate Newtonian dynamics, it would also violate Milgromian dynamics and perhaps everything we know about electromagnetism.
Speculative claims
One researcher named Norbert Klein has claimed to find laboratory evidence for a MOND-like modification of gravity. He does so based on just three data points from Cavendish-like experiments that measure Newton’s constant G and that don’t quite agree with one another. This constant appears in both Newtonian gravity and Milgromian gravity and is vital for calculating the strength of the gravitational fields. It is difficult to measure with precision because gravity is a very weak force compared to the other forces of nature. Klein’s suggestion is highly controversial however because Klein uses only a very small selection of the total available gravitational experiments. The experts in the field state that the tiny differences in the measurements of Newton’s constant between different experiments are most likely due to systematic errors.
Other similar claims that Newton’s constant varies are also unlikely to be true based on more accurate analyses. The best evidence that Newton’s constant doesn’t change comes from observations of type Ia supernovae. These happened in the universe’s remote past and paired with the assumption that the physics involved in these events is universal, such supernovae show that Newton’s constant cannot have changed by more than 1 part in 10 billion per year over the last nine billion years.




Leave a Reply